How to Trade Earnings Announcement?
There is an old saying on Wall Street that “earnings drive stock prices”. A good example is Nvidia’s (NASDAQ: NVDA) earnings announcement after the market close on May 24, 2023. If you are not familiar with earnings announcement, check out our article What is Earnings Announcement.
During this event, Nvidia reported its first-quarter performance for fiscal 2024. The company announced earnings that exceeded expectations and forecasted a surge in revenue from AI chip demand. This news immediately drove the stock price up by as much as 26% in extended trading, reaching an all-time high.
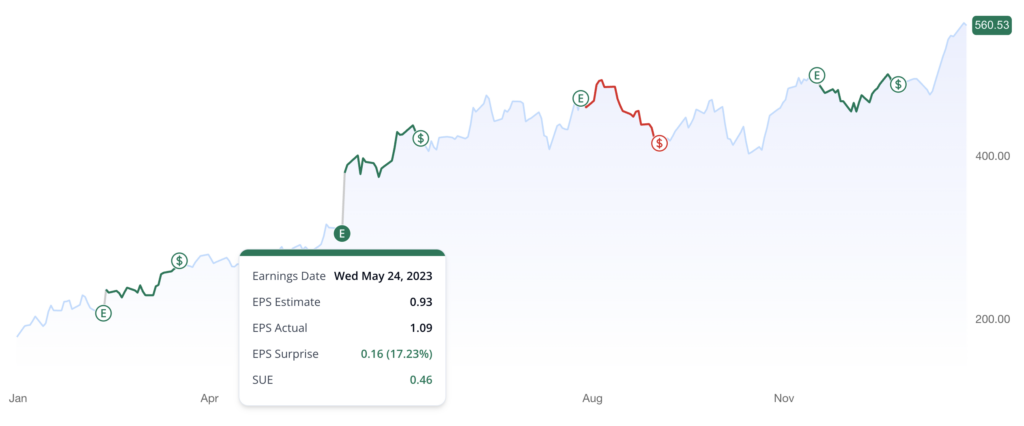
What information sparked the change in the stock price? In which direction did the price move? How can we leverage this situation to profit? How long should we maintain our investment position?
Interestingly, when a company’s earnings differ from expectations, its stock price typically moves in the same direction as the earnings surprise. This effect isn’t limited to just one day; it can persist for several weeks or even 3 to 6 months after the earnings announcement. This phenomenon is known as “Post-Earnings Announcement Drift” or PEAD. In this article, we will delve into PEAD in more detail.
Post-Earnings Announcement Drift (PEAD)
The Post-Earnings Announcement Drift (PEAD) was first found by Ball and Brown in 1968 (Ball & Brown, 1968). They observed that stocks with better-than-expected earnings tend to go up in the three months following the announcement. Meanwhile, while those with unexpected losses tend to decline in the same period.
Since Ball and Brown’s discovery, many researchers have studied PEAD and confirmed that it is not a random occurrence; rather, it remains a consistent and prominent phenomenon in the stock market that generates excessive returns even today (Bond et al., 2023; Choi et al., 2023; Fink, 2021).
Fama (1998) referred to PEAD as the “grand-daddy of under-reaction events”, highlighting it as one of the most baffling anomalies in the stock market.
Over 50 years of research on PEAD has resulted in more than 1,000 academic papers. Most of these studies indicate that PEAD typically occurs within three months, with some findings suggesting it can last up to six months. Moreover, PEAD is a global phenomenon, occurring in stock markets around the world.
Earnings Measurement
What caused the stock price to change after the earnings were announced? Instead of trying to figure this out on our own right away, it’s easier if we learn from the experts. Let’s start by checking out what others have found important about PEAD.
Earnings Surprise %
This is a widely used number to measure “surprise” in earnings announcement on websites like Google and Yahoo Finance. It is calculated as follows:
where is the Earnings per share (EPS) reported by the company during the earnings announcement. EPS represents a company’s net profit (or loss) divided by the number of outstanding shares of common stock, indicating how much money a company makes per share of its stock and serving as a crucial indicator of company value. is the EPS estimated by analysts before earnings. Thus, earnings surprise measures the difference between reported EPS and estimated EPS.
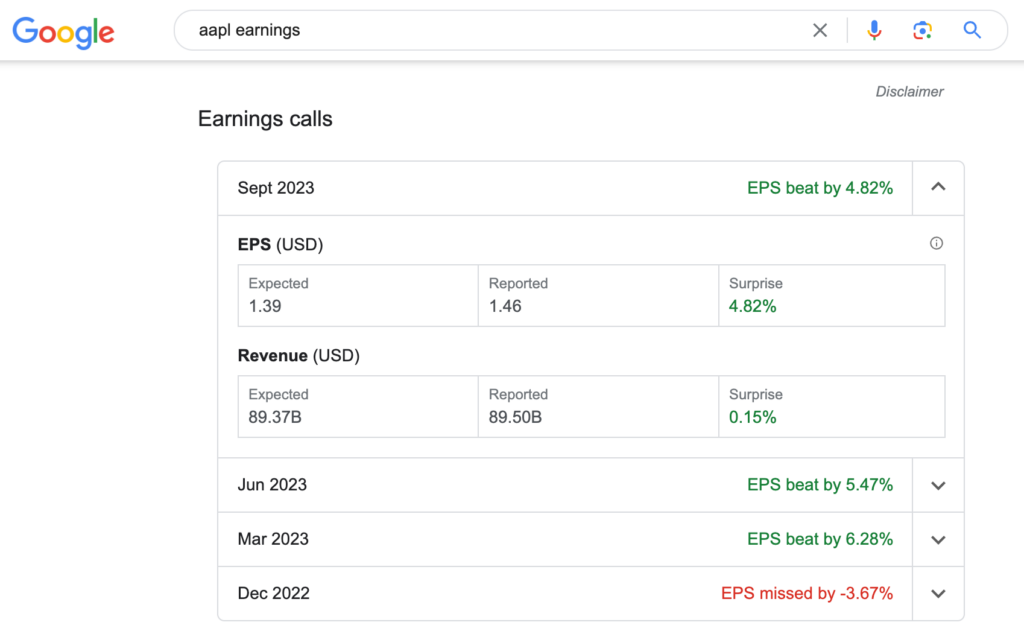
For example, consider Apple Inc’s earnings for September 2023. Google shows the surprise as .
Analysts use various methods to formulate their estimates, such as quantitative forecasting models, input from the company’s management, industry conditions, and other information to make an educated guess on EPS.
However, this approach has limitations. For instance, the surprise percentage can be meaningless if the estimated EPS is close to zero.
Additionally, comparing this number across companies is challenging due to differences in the historical variability of earnings surprises.
Let’s look at two companies, A and B, both of which had a 10% earnings surprise in the latest quarter. However, if Company A usually has small earnings surprises, around 1%, and Company B often has much larger surprises, like 40%, then Company A’s surprise seems more significant compared to its normal performance than Company B’s does.
Standardized Unexpected Earnings (SUE)
To account for historical variability of earnings surprises, a measure known as “Standardized Unexpected Earnings” can be used (Ball & Brown, 1968). The formula is:
where is standardized unexpected earnings for the quarter, is the actual EPS reported by the firm, is the forecasted EPS. is the standard deviation of the difference (surprise) between actual and forecasted EPS, usually calculated over the prior 8-12 quarters.
Note that standard deviation is a number to tell how spread out the values of multiple numbers are from its average value. If the standard deviation is low, it means that the values are mostly close to the average. If it’s high, the values are more scattered and cover a wider range.
Let’s use the analyst forecast as to calculate . Assuming the following EPS data for a stock and the standard deviation of the unexpected earnings calculated over the last eight quarters, the for the quarter ending in September 2023 is 1.50.
data
| eps_actual | eps_estimate | |
|---|---|---|
| quarter_ending | ||
| 201209 | 1.20 | 1.16 |
| 201212 | 1.09 | 1.05 |
| 201303 | 0.77 | 0.71 |
| 201306 | 1.31 | 1.19 |
| 201309 | 1.24 | 1.17 |
| 201312 | 1.05 | 1.00 |
| 201403 | 0.83 | 0.75 |
| 201406 | 1.32 | 1.23 |
| 201409 | 1.36 | 1.29 |
| 201412 | 1.12 | 1.08 |
| 201503 | 0.83 | 0.79 |
| 201506 | 1.32 | 1.23 |
| 201509 | 1.35 | 1.26 |
| 201512 | 1.06 | 1.06 |
| 201603 | 0.89 | 0.81 |
| 201606 | 1.35 | 1.28 |
| 201609 | 1.40 | 1.32 |
| 201612 | 1.20 | 1.16 |
| 201703 | 0.94 | 0.91 |
| 201706 | 1.50 | 1.39 |
| 201709 | 1.48 | 1.42 |
| 201712 | 1.31 | 1.30 |
| 201803 | 0.96 | 0.92 |
| 201806 | 1.61 | 1.51 |
| 201809 | 1.59 | 1.56 |
| 201812 | 1.49 | 1.49 |
| 201903 | 0.97 | 0.92 |
| 201906 | 1.54 | 1.49 |
| 201909 | 1.56 | 1.50 |
| 201912 | 1.45 | 1.43 |
| 202003 | 1.07 | 1.02 |
| 202006 | 1.32 | 1.25 |
| 202009 | 1.66 | 1.48 |
| 202012 | 1.47 | 1.45 |
| 202103 | 1.21 | 1.12 |
| 202106 | 1.72 | 1.52 |
| 202109 | 1.79 | 1.73 |
| 202112 | 1.53 | 1.53 |
| 202203 | 1.29 | 1.24 |
| 202206 | 1.86 | 1.73 |
| 202209 | 1.97 | 1.85 |
| 202212 | 1.67 | 1.64 |
| 202303 | 1.50 | 1.37 |
| 202306 | 2.09 | 1.95 |
| 202309 | 2.25 | 2.17 |
(2.25-2.17)/(data['eps_actual']-data['eps_estimate']).tail(8).std()
1.5042028661807123
SUE measures the earnings surprise in terms of standard deviation above or below the consensus earnings estimate.
The absolute value of SUE measures the degree of unexpected earnings, while the sign of SUE shows whether the unexpected earnings are above or below the estimate. In other words, a higher positive SUE indicates a greater earnings surprise above the estimate, while a smaller negative SUE indicates a greater surprise below the estimate. When SUE equals zero, there is no earnings surprise, and the actual EPS aligns with the estimate.
Since analysts often use quantitative models to forecast earnings, can we do the same? Absolutely! Let’s review some models that people use.
1. Seasonal Model
This simple method is commonly used by researchers (Chan et al., 1996). Since earnings often follow a seasonal pattern, we can estimate EPS as the actual EPS from four quarters ago (the same quarter in the last year):
For example, using the previous EPS data, the EPS for the quarter ending in December 2023 will be estimated as 1.67, the same as the actual EPS of December 2022 quarter.
2. Seasonal Model with a Trend Factor
This model adds a “trend factor” by considering how earnings have changed historically (Bernard & Thomas, 1990; Foster, 1977) , and it can be more accurate than the simple seasonal model. It’s based on the idea that “Last year’s earnings were this much, and on average, they tend to grow or shrink by this amount over time.”
Researchers usually look back 8 to 20 quarters, or over all available history, to calculate the trend factor.
For example, using the previous EPS data, the trend factor calculated over all available data is:
(data['eps_actual']-data['eps_actual'].shift(4)).mean()
0.07658536585365854
In this case, the EPS for the December 2023 quarter will be estimated as the EPS of the December 2022 quarter plus trend, which equals 1.67 + 0.08 = 1.75
3. Autoregressive Model
Autoregressive time series models assume that earnings are related not only to the same quarter in the previous year but also to adjacent quarters (Brown & Rozeff, 1979; Foster, 1977). For example, Brown & Rozeff ARIMA (1,0,0) X (0,1,1) model assumes that earnings follow a first-order autoregressive process,
where is the autoregressive coefficient estimated from historical data, and are seasonal moving average parameters, and is the disturbance term at time t-4. As this model is the most complex, we use a Python package called statsmodels to estimate the model.
from statsmodels.tsa.statespace.sarimax import SARIMAX
def model_brown(eps_actual):
model = SARIMAX(eps_actual, order=(1,0,0), seasonal_order=(0,1,1,4))
results = model.fit(disp=False)
yhat = results.forecast(1)
return yhat
model_brown(data['eps_actual']).iloc[0]
1.8486443674803033
In this case, we estimate the model parameters using all available historical data. The EPS for quarter ending in December 2023 will be estimated as 1.85.
Let’s compare these estimates for a stock in the following figure. Firstly, the figure clearly shows that EPS has seasonality. Secondly, it appears that all three models and the analyst forecast closely track the actual EPS for this stock.
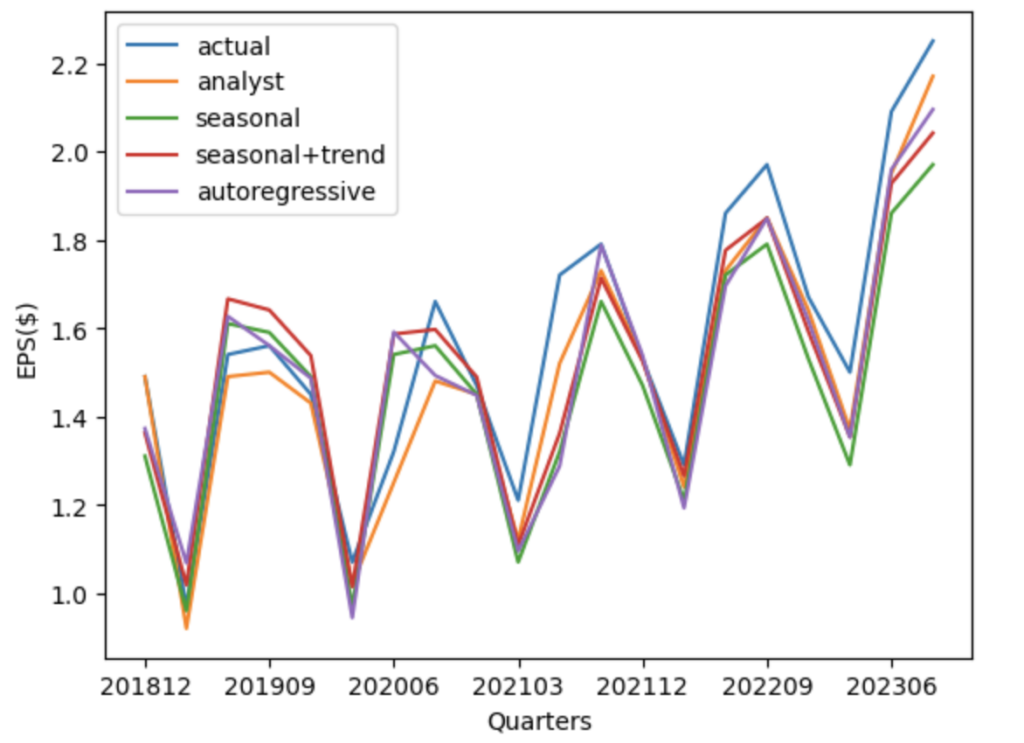
Foster (1977) found that an ARIMA (1,0,0) X (0,1,0) autoregressive model generally produces more accurate forecasts than the seasonal models.
Foster et al. (1984) applied both seasonal model and autoregressive model to calculate SUE and examined stock performance 60 days after earnings announcements. They found significant PEAD: stocks tend to perform better after the announcement if the SUE is positive and larger, and worse if the SUE is negative and smaller.
In simple terms, if a company surprises everyone with better-than-expected earnings, its stock tends to go up after the announcement. Conversely, if it surprises with worse-than-expected earnings, the stock tends to underperform.
Bernard & Thomas (1990) ranked stocks by SUE, bought those with the highest SUE, sold those with the lowest SUE, and held them for 60 days (3 months), achieving 18% abnormal returns.
Livnat & Mendenhall (2006) compared forecasts from analysts and models and found that the abnormal returns for long and short positions are 3.6% with the autoregressive time series model, but 4.4% with the analyst forecast model, which is 0.8% higher. Additionally, these two methods don’t fully explain each other, as only 50% of the stocks are the same in the highest or lowest groups. Combining both models could yield a higher abnormal return (6.9%).
Pagach & Warr (2020) found that the differences in forecast accuracy between analysts and the Brown & Rozeff autoregressive model are small. Specifically, the autoregressive model’s forecasts are more accurate (or equally accurate) than those of analysts 40% of the time for one-quarter ahead predictions. For high-technology firms, the autoregressive model beats (ties or beats) the analyst 41% (48%) of the time for three-quarter-ahead forecasts.
Autoregressive time series models are likely to work best for firms with a long history of earnings and where the parameters of the models have not significantly shifted over time.
Standardized Unexpected Revenue (SUR)
Besides earnings per share (EPS), companies also report revenue during earnings announcement. There can be differences or surprises between reported revenue and forecasted revenue. Since profit equals revenue minus expenses, this method argues that earnings surprises are more influenced by revenue surprises than by expense surprises.
Jegadeesh & Livnat (2006) used a method similar to the seasonal model with a trend factor to calculate Standardized Unexpected Revenue (SUR). They found that SUR can indeed predict future profit growth. Stocks with high unexpected revenue generate higher positive abnormal returns both before and after earnings announcements, while those with low unexpected revenue experience lower and negative excess returns.
Earnings Announcement Return (EAR)
Earnings Announcement return (EAR) is another commonly used metric in addition to SUE. EAR is the difference of return around the time of the earnings announcement between the stock return and the return of a portfolio of stocks with similar risk exposures. It attempts to capture the surprise in all aspects of the company’s earnings announcement, and not just the surprise in earnings per share (EPS).
For example, Chan et al. (1996) calculated EAR using the sum of stock abnormal returns from two days before the earnings announcement date to one day after. The abnormal return is the stock return minus the return of an equally-weighted market index. They found that EAR methods could generate excess returns over 6-12 months.
Kishore et al. (2008) defined EAR as abnormal return over a three-day window centered on the announcement date, using a benchmark portfolio to calculate expected returns. Their findings showed that buying and selling companies sorted on EAR produces an average abnormal return of 6.3% per year, which is 0.6% more than a strategy based on the traditional measure of earnings surprise.
Unexpected Trading Volume
Unexpected trading volume measures abnormal trading volume over a two-day window around the announcement date, compared to typical trading volume during a non-announcement period (Garfinkel & Sokobin, 2006; Gerard, 2012).
At the time of earnings announcements, unexpected trading volume seems to positively correlate with future returns. This means that higher opinion divergence at the time of the earnings announcement is associated with more positive returns in the period following the announcement.
Jump
“Jump” measures how stock prices react abruptly to major events such as earnings announcement. If a company’s financial data surprises the market, you might see a gap in stock prices – either up or down. Jump is about capturing these sudden price changes.
It is assumed that companies’ unobserved “extremely good news” is reflected in unexpectedly large and discrete price hikes, or positive jumps, around earnings announcements. Conversely, companies’ unobserved “extremely bad news” is shown in large and abrupt price plunges, or negative jumps, around these times (Zhou & Zhu, 2012).
Simply put, “jump” can be defined as the difference between the opening price on the next trading day and the previous day’s closing price:
If the stock price jumps significantly higher on the next trading day after earnings announcement, it suggests that the earnings data is better than expected. On the other hand, if the stock price drops significantly, it indicates that the earnings data might be worse than expected.
Zhou & Zhu (2012) also proposed another way to calculate jump over a three-day window centered on earnings announcement dates, using the L statistic. Based on this metric’s sign, they developed a strategy that took long or short positions in stocks on day t + 2 in stocks and held them for three months. This strategy yielded a quarterly excess return of 3.63%, equivalent to an annualized return of 15.3%, over the sample period.
Observations
In the early days, some attributed the PEAD effect on improper data handling and research processes. However, as research showed that the PEAD effect existed across countries and time periods, it couldn’t be attributed to chance or data mining anymore.
PEAD and Company Size
The PEAD effect is stronger for smaller companies. While it occurs in companies of all sizes, studies (Bernard & Thomas, 1990; Foster et al., 1984) have shown that the bigger the company, the smaller the abnormal returns tend to be. This is partly because smaller companies often face higher trading difficulties and have less clear information. It is believed that company size isn’t the only factor, but it remains a useful representation of various other factors.
Bhushan (1994) looked at the relationship between PEAD and company size from the perspective of trading costs. Since stock prices and trading volume can represent the level of trading costs, these variables are related to a company’s market size. Generally, companies with larger market capitalizations have higher stock prices and greater trading volumes, while those with smaller market capitalizations have lower stock prices and less trading activity.
PEAD and Trading Cost
The PEAD effect is more significant in stocks with higher trading costs, including bid-ask spreads, commissions, and illiquidity (Chordia et al., 2009). For an individual stock, liquidity reflects how easily and cost-effectively investors can buy or sell shares without significantly impacting the market. Since liquidity is inversely related to company size, this aligns with the observation of the relationship between company size and PEAD.
Amihud (2002) found that the profit from a long-short strategy, which involves buying high SUE stocks and selling low SUE stocks, increases with illiquidity. In the group with the most liquid stocks, this long-short strategy yields only a 0.04% monthly profit, while in the group with the least liquid stocks, it yields a 2.43% monthly profit. This indicates that the SUE strategy is more effective with stocks that are harder to trade and less so with those easily traded.
PEAD and Institutional Ownership
The PEAD effect is weaker in stocks with higher institutional ownership (Bartov et al., 2000). The more institutional investors present, the less pronounced the PEAD effect. Conversely, with fewer institutional investors, the PEAD effect becomes more noticeable.
Institutional investors are often well-informed and anticipate earnings surprises. Following the announcement, they typically increase their investment in stocks with positive news and decrease it in stocks with negative news.
Potential Explanations
Inadequate Response
Investors have limited capacity to process information, and when facing a lot of information simultaneously, they have to choose what to focus on. This is especially true during earnings announcements, which contain a lot of information. Investors might become
overwhelmed and fail to immediately absorb and process the new information in unexpected earnings, leading to a pronounced inadequate response and the PEAD effect.
DellaVigna & Pollet (2009) compared announcements that occur on Friday with those on other weekdays. They assumed that if weekends distract investors and lower the quality of decision-making, the immediate response to Friday earnings surprises should be less pronounced. Indeed, they found that earnings announcements on Fridays had a weaker market impact, likely because investors are less attentive on those days.
Limits to Arbitrage
PEAD effect may continue to exist due to limits to arbitrage caused by transaction costs. When transaction costs are low, informed investors might quickly arbitrage away any mispricing. In contrast, when transaction costs are high, arbitrageurs may refrain from trading until the potential profit from mispricing becomes large enough.
During earnings announcements, an underreaction to earnings can occur because transaction costs restrict the profitable trades of informed investors. Ng et al. (2008) found that the drift in returns following earnings surprises is larger for firms with higher transaction costs for their shares, clearly demonstrating the impact of transaction costs on the persistence of the PEAD effect.
Next Step
So far, we have gained a basic understanding of what Post-Earnings Announcement Drift (PEAD) is and how people have found it useful for making a profit.
It is important to understand why the PEAD effect exists and in what situations it will continue to persist in the foreseeable future.
In the next step, we are going to conduct some studies and build trading strategies based on recent data.
References
Amihud, Y. (2002). Illiquidity and stock returns: cross-section and time-series effects. Journal of financial markets, 5(1), 31-56.
Ball, R., & Brown, P. (1968). Empirical Evaluation Of Accounting Income Numbers. Journal of Accounting Research, 6, 159-178.
Bartov, E., Radhakrishnan, S., & Krinsky, I. (2000). Investor sophistication and patterns in stock returns after earnings announcements. The accounting review, 75(1), 43-63.
Bernard, V. L., & Thomas, J. K. (1990). Evidence that stock prices do not fully reflect the implications of current earnings for future earnings. Journal of accounting and economics, 13(4), 305-340.
Bhushan, R. (1994). An informational efficiency perspective on the post-earnings announcement drift. Journal of accounting and economics, 18(1), 45-65.
Bond, S., Wu, W., & Zheng, S. (2023). Seasonal patterns of earnings releases and post-earnings announcement drift. The Quarterly Review of Economics and Finance, 91, 15-24.
Brown, L. D., & Rozeff, M. S. (1979). Univariate time-series models of quarterly accounting earnings per share: A proposed model. Journal of Accounting Research, 179-189.
Chan, L. K., Jegadeesh, N., & Lakonishok, J. (1996). Momentum strategies. The journal of Finance, 51(5), 1681-1713.
Choi, L., Faurel, L., & Hillegeist, S. A. (2023). Insider trading, future earnings, and post-earnings announcement drift. Journal of Accounting and Public Policy, 42(4), 107117.
Chordia, T., Goyal, A., Sadka, G., Sadka, R., & Shivakumar, L. (2009). Liquidity and the post-earnings-announcement drift. Financial Analysts Journal, 65(4), 18-32.
DellaVigna, S., & Pollet, J. M. (2009). Investor inattention and Friday earnings announcements. The journal of Finance, 64(2), 709-749.
Fama, E. F. (1998). Market efficiency, long-term returns, and behavioral finance. Journal of financial economics, 49(3), 283-306.
Fink, J. (2021). A review of the post-earnings-announcement drift. Journal of Behavioral and Experimental Finance, 29, 100446.
Foster, G. (1977). Quarterly accounting data: Time-series properties and predictive-ability results. Accounting Review, 1-21.
Foster, G., Olsen, C., & Shevlin, T. (1984). Earnings releases, anomalies, and the behavior of security returns. Accounting Review, 574-603.
Garfinkel, J. A., & Sokobin, J. (2006). Volume, opinion divergence, and returns: A study of post–earnings announcement drift. Journal of Accounting Research, 44(1), 85-112.
Gerard, X. (2012). Information Uncertainty and the Post–Earnings Announcement Drift in Europe. Financial Analysts Journal, 68(2), 51-69.
Jegadeesh, N., & Livnat, J. (2006). Post-earnings-announcement drift: The role of revenue surprises. Financial Analysts Journal, 22-34.
Kishore, R., Brandt, M. W., Santa-Clara, P., & Venkatachalam, M. (2008). Earnings announcements are full of surprises. Available at SSRN 909563.
Livnat, J., & Mendenhall, R. R. (2006). Comparing the post–earnings announcement drift for surprises calculated from analyst and time series forecasts. Journal of Accounting Research, 44(1), 177-205.
Ng, J., Rusticus, T. O., & Verdi, R. S. (2008). Implications of transaction costs for the post–earnings announcement drift. Journal of Accounting Research, 46(3), 661-696.
Pagach, D. P., & Warr, R. S. (2020). Analysts versus time-series forecasts of quarterly earnings: A maintained hypothesis revisited. Advances in accounting, 51, 100497.
Zhou, H., & Zhu, J. Q. (2012). Jump On The Post-Earnings Announcement Drift. Financial Analysts Journal, 68(2), 63.